dummy slide

Personalizing drug doses
in the cloud using R
Gergely Daróczi
Co-founder, CTO
Rx Studio Inc.
$ whoami
$ whoami
$ whoami
$ whoami
$ whoami
$ whoami
$ pwd
$ lsb_release

$ lsb_release

Source:
When
my co-worker wants to simplify code
that took two days to
understand
> Sys.getenv(country = ‘USA’)
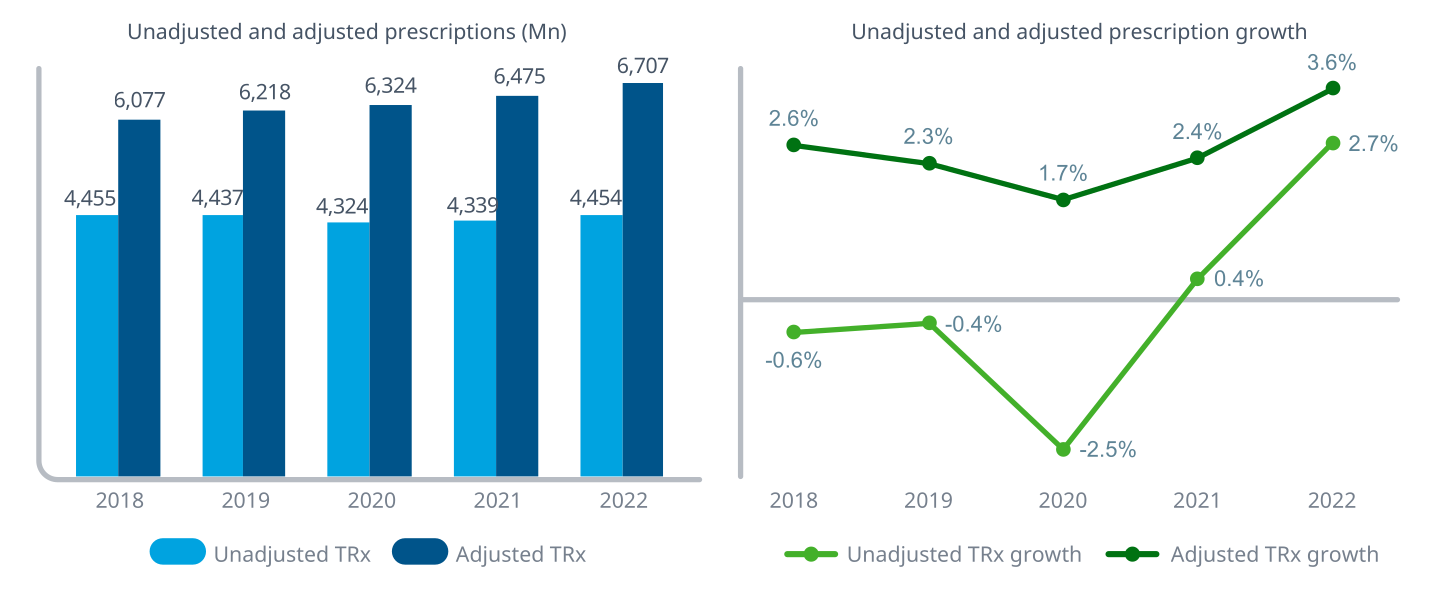
Source: The Use of Medicines in the U.S. 2023 (IQVIA)
> Sys.getenv(country = ‘USA’)
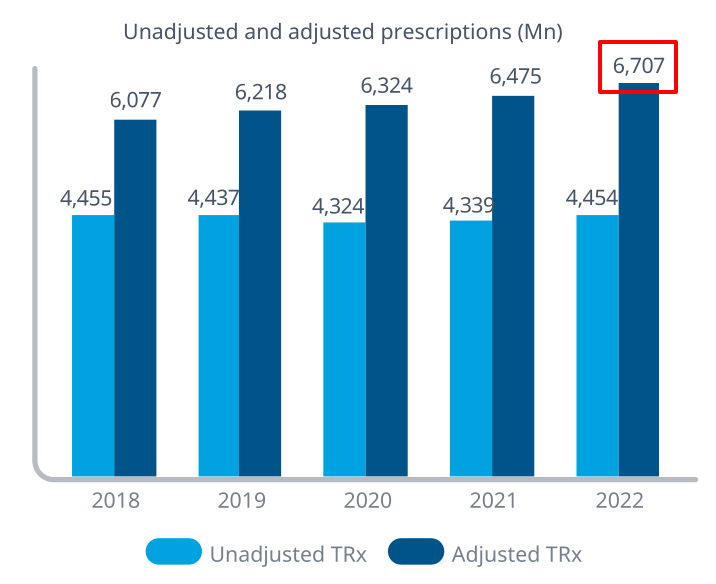
> Sys.getenv(country = ‘USA’)
The estimated annual cost of prescription drug–related morbidity and mortality resulting from nonoptimized medication therapy was $528.4 billion in 2016 US dollars. Watanabe et al, 2018 (doi.org/10.1177/10600280187651)
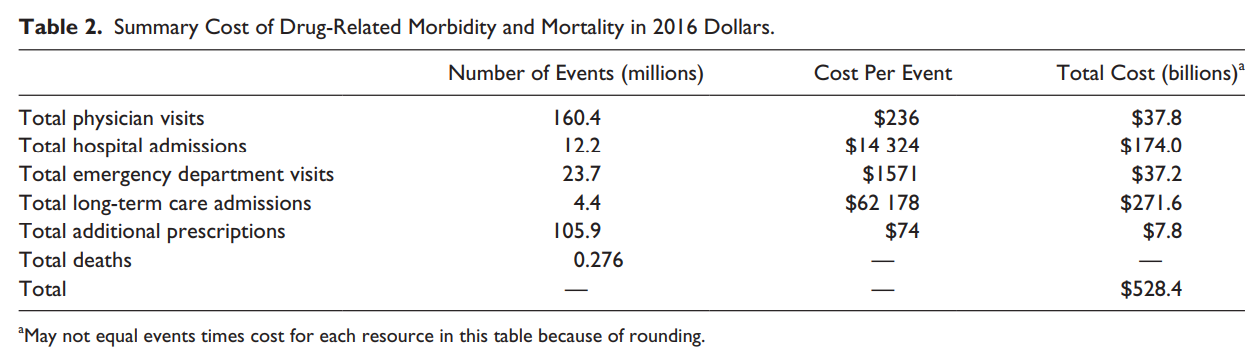
> Sys.getenv(country = ‘USA’)

If medications were prescribed, monitored and taken properly,
we wouldn’t face this cost, and patients would be healthier. Watanabe et al, 2018 (doi.org/10.1177/10600280187651)
> ??properly
> ??properly

> demo(‘rx.studio’)
> vignette(topic = ‘PK/PD models’)
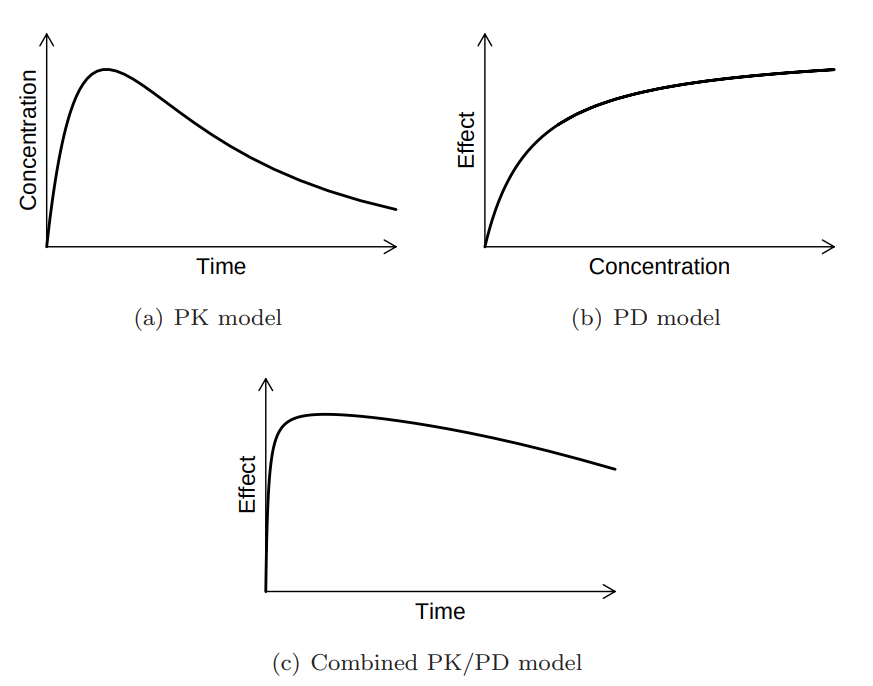
> vignette(topic = ‘PK/PD models’)




Source: Mortensen et al (2008): Introduction to PK/PD modelling.
> vignette(topic = ‘PK/PD models’)

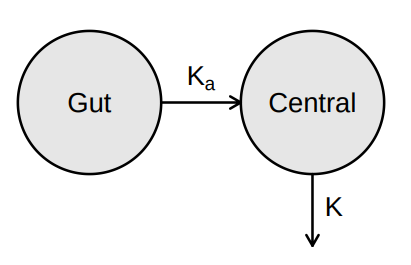


Source: Mortensen et al (2008): Introduction to PK/PD modelling.
> vignette(topic = ‘PK/PD models’)


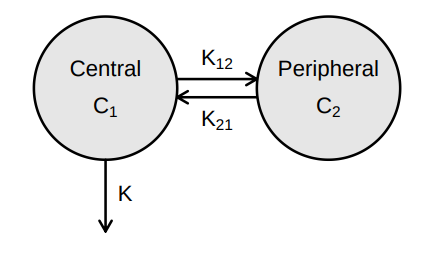

Source: Mortensen et al (2008): Introduction to PK/PD modelling.
> vignette(topic = ‘PK/PD models’)



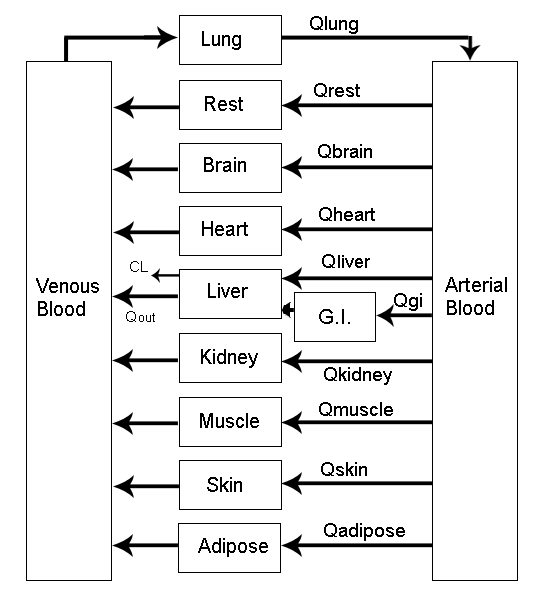
Source: Mortensen et al (2008): Introduction to PK/PD modelling.
> vignette(topic = ‘PK/PD models’)

Source: Spherical cow
> vignette(topic = ‘PK/PD models’)
> vignette(topic = ‘PK/PD models’)

\[C=\frac{A}{V}\]
- \(C\) drug concentration
- \(A\) drug amount
- \(V\) volume of distribution
Example: 500 mg Panadol (\(Vd = 0.9L/kg\)) administered for a 70 kg patient
\[C=\frac{500mg}{70kg * 0.9L/kg}=\frac{500mg}{63L}=7.9 mg/L\]
> vignette(topic = ‘PK/PD models’)

> vignette(topic = ‘PK/PD models’)

\[C_{oral}(t)=\frac{A_{oral}(t)}{V}=\frac{K_aFA_0}{V(K_a-K)}(exp(-K \cdot t) - exp(-K_a \cdot t))\]
- \(C\) drug concentration
- \(A\) drug amount
- \(V\) volume of distribution
- \(K_a\) absorption constant
- \(K\) elimination rate
- \(F\) bioavailability
> vignette(topic = ‘PK/PD models’)

\[C_{oral}(t)=\frac{A_{oral}(t)}{V}=\frac{K_aFA_0}{V(K_a-K)}(exp(-K \cdot t) - exp(-K_a \cdot t))\]
#' Concentration at a time computed using a one-compartment model (oral dose)
#' @param t time (hours)
#' @param dose dose amount (mg)
#' @param v volume of distribution (l)
#' @param k elimination rate constant (h^-1)
#' @param ka absorption rate constant (h^-1)
#' @param f bioavailability
#' @return numeric
#' @export
ct <- function(t, dose, v, k, ka, f) {
(ka * f * dose) / (v * (ka - k)) * (exp(-k * t) - exp(-ka * t))
}> example(topic = ‘paracetamol’)

Source: Rawlins et al. (1977): Paracetamol (simplified)
> example(topic = ‘paracetamol’)

Source: Rawlins et al. (1977): Paracetamol (simplified)
> example(topic = ‘paracetamol’)
#' Concentration at a time computed using a one-compartment model (oral dose)
#' @param t time (hours)
#' @param dose dose amount (mg)
#' @param v volume of distribution (l)
#' @param k elimination rate constant (h^-1)
#' @param ka absorption rate constant (h^-1)
#' @param f bioavailability
#' @return numeric
#' @export
ct <- function(t, dose, v, k, ka, f) {
(ka * f * dose) / (v * (ka - k)) * (exp(-k * t) - exp(-ka * t))
}> example(topic = ‘paracetamol’)
#' Concentration at a time computed using a one-compartment model (oral dose)
#' @param t time (hours)
#' @param dose dose amount (mg)
#' @param v volume of distribution (l)
#' @param k elimination rate constant (h^-1)
#' @param ka absorption rate constant (h^-1)
#' @param f bioavailability
#' @return numeric
#' @export
ct <- function(t, dose, v, k, ka, f) {
(ka * f * dose) / (v * (ka - k)) * (exp(-k * t) - exp(-ka * t))
}> example(topic = ‘paracetamol’)
#' Concentration at a time computed using a one-compartment model (oral dose)
#' @param t time (hours)
#' @param dose dose amount (mg)
#' @param v volume of distribution (l)
#' @param k elimination rate constant (h^-1)
#' @param ka absorption rate constant (h^-1)
#' @param f bioavailability
#' @return numeric
#' @export
ct <- function(t, dose, v, k, ka, f) {
(ka * f * dose) / (v * (ka - k)) * (exp(-k * t) - exp(-ka * t))
}> example(topic = ‘paracetamol’)
library(data.table); library(ggplot2)
conc <- data.table(h = seq(0, 24, by = 0.1))
conc[, c := ctp(h, 1000)]
ggplot(conc, aes(h, c)) + geom_line()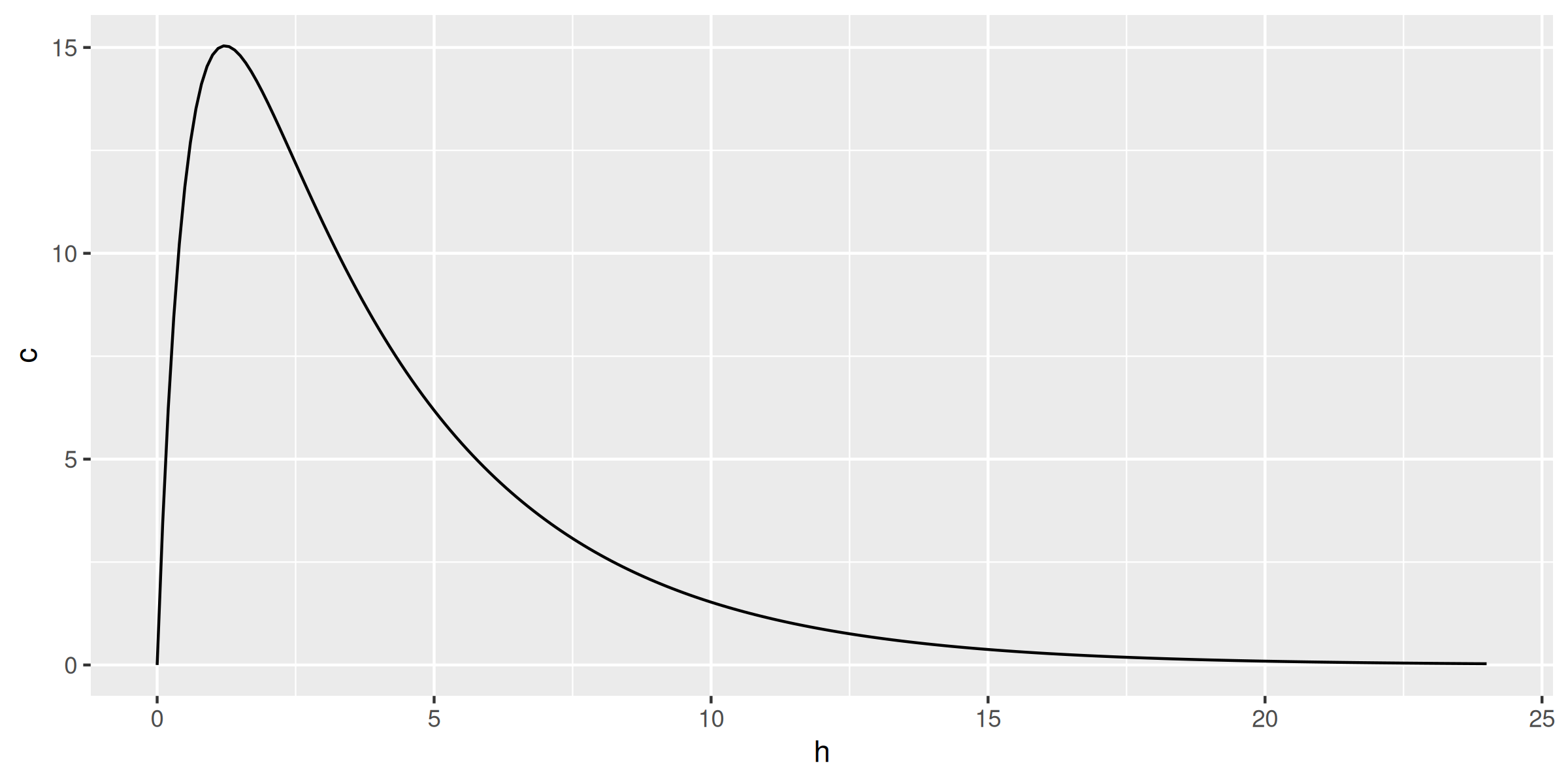
> do.call(ctp, weights)
ctp <- function(t, dose, weight, k = 0.28, ka = 1.8, f = 0.89) {
ct(t, dose, v = weight * 0.6, k, ka, f)
}conc[, c1 := ctp(h, 1000, weight = 40)]
conc[, c2 := ctp(h, 1000, weight = 60)]
conc[, c3 := ctp(h, 1000, weight = 80)]
conc[, c4 := ctp(h, 1000, weight = 100)]
ggplot(melt(conc, id.vars = 'h'), aes(h, value, color = variable)) +
geom_line() +
scale_color_discrete(name = 'Weight',
labels = c('40 kg', '60 kg', '80 kg', '100kg')) +
ylab('Blood concentration forecast') +
theme(legend.position = 'top') +
geom_hline(yintercept = 10, color = 'black', linetype = 2, size = 1.25) +
geom_hline(yintercept = 20, color = 'black', linetype = 2, size = 1.25)> do.call(ctp, weights)

> do.call(ctp, family)
An anonymized family:
- GD (96 kg male): 1 pill of Panadol (500 mg)
- HD (64 kg female): 1 pill of Panadol (500 mg)
- BD (41 kg male): 1 pill of Panadol (500 mg)
- BD (23 kg female): half pill of Panadol (250 mg)
- BD (13 kg female):
7-85ml Panadol baby (120 mg)
Therapeutic goals for paracetamol:
- sub-therapeutic range: < 10 mg/L concentrations
- therapeutic range: ≥ 10 and ≤ 20 mg/L concentrations
- toxic: > 75 mg/L concentrations
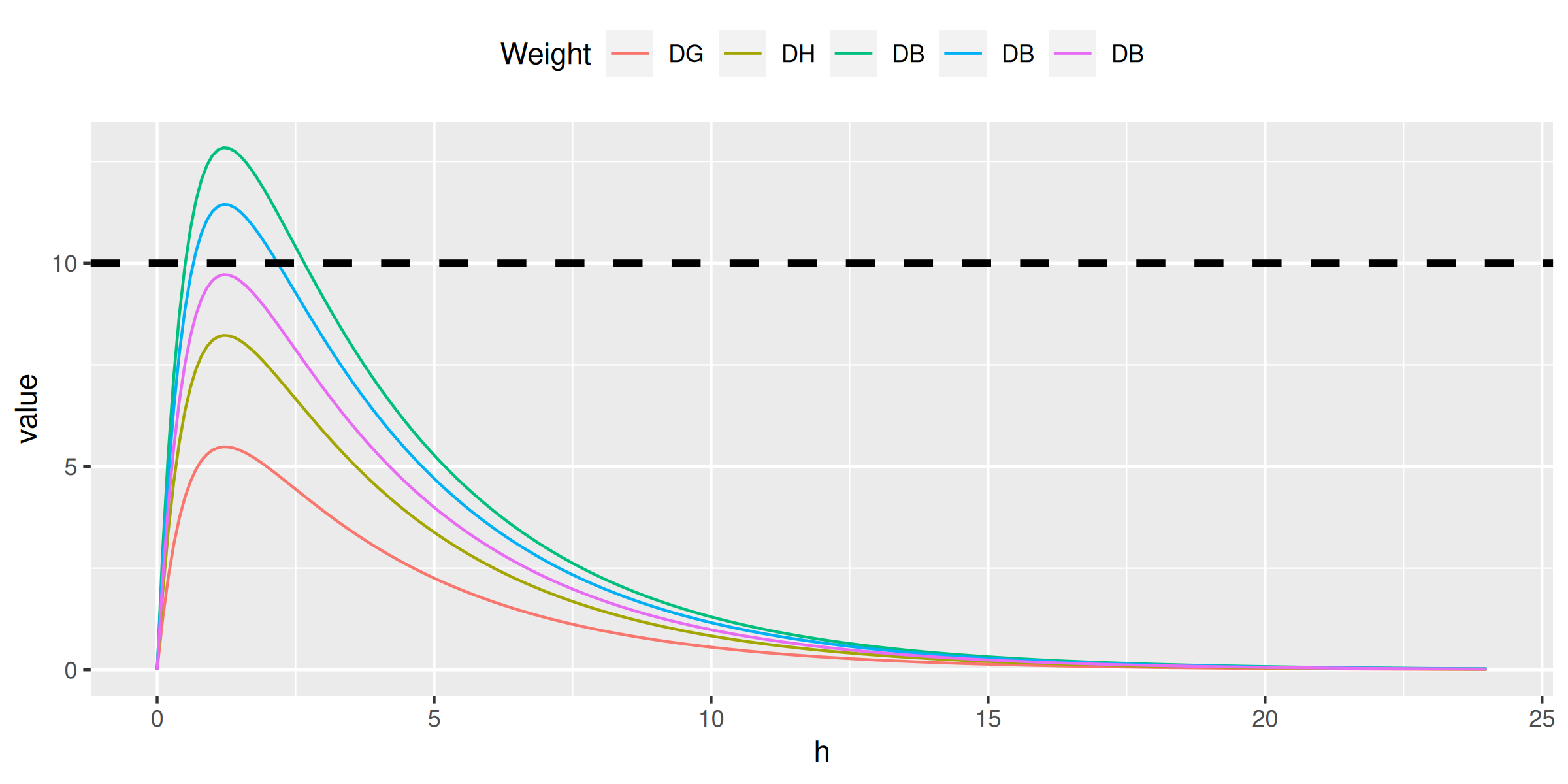
> do.call(ctp, family)
conc[, c1 := ctp(h, 500, weight = 96)]
conc[, c2 := ctp(h, 500, weight = 64)]
conc[, c3 := ctp(h, 500, weight = 41)]
conc[, c4 := ctp(h, 250, weight = 23)]
conc[, c5 := ctp(h, 120, weight = 13)]
ggplot(melt(conc, id.vars = 'h'), aes(h, value, color = variable)) + geom_line() +
scale_color_discrete(name = 'Weight', labels = c('DG', 'DH', 'DB', 'DB', 'DB')) +
theme(legend.position = 'top') +
geom_hline(yintercept = 10, color = 'black', linetype = 2, size = 1.25)> do.call(ctp, family)
> do.call(ctp, family, ndoses = 4)
\[C_{MD}(t)=\sum_{n=0}^{N-1} C_{oral}(t-nτ)\]
- \(N\) number of doses
- \(τ\) dosing interval
Source: Mortensen et al (2008): Introduction to PK/PD modelling.
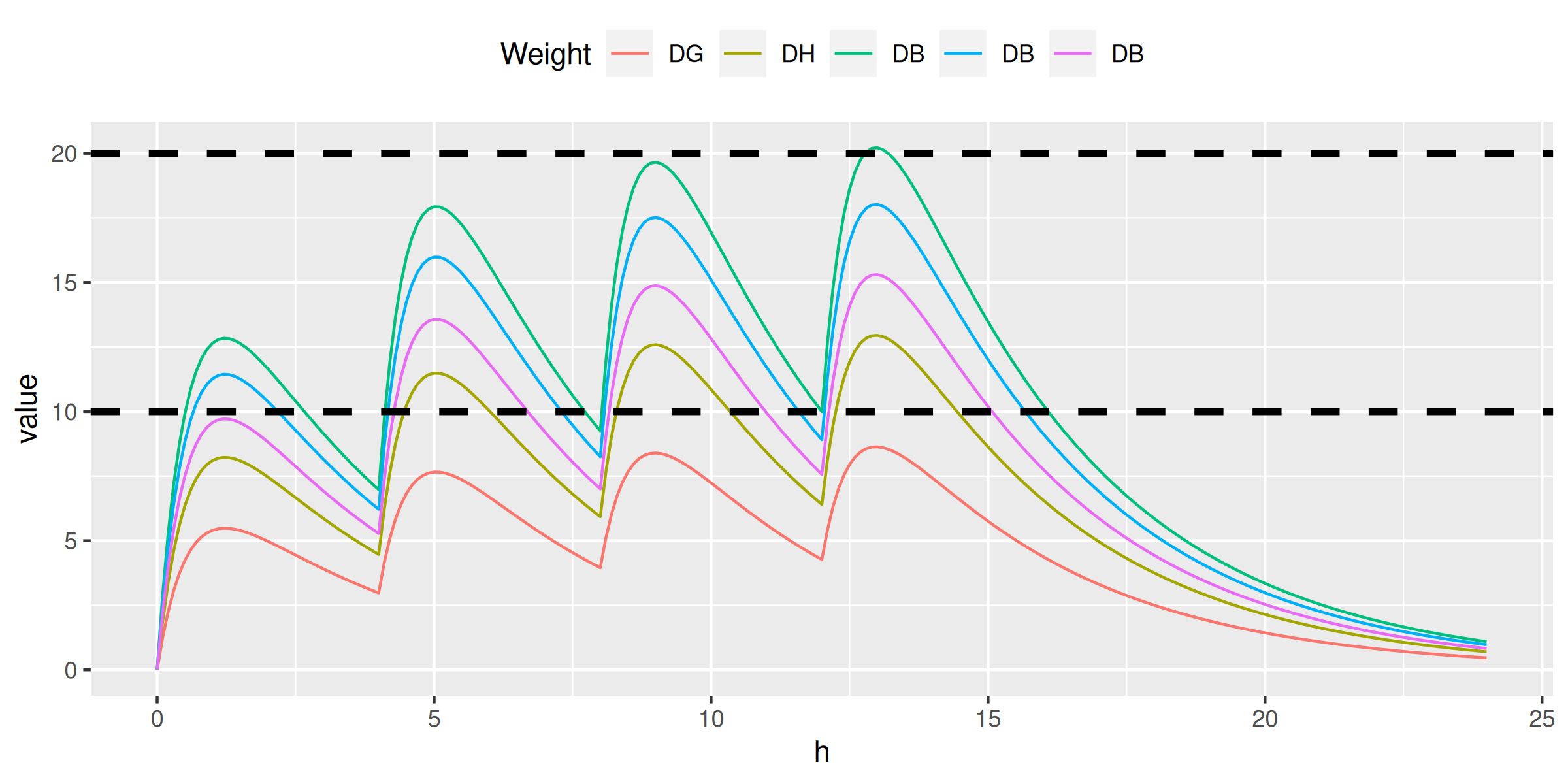
> do.call(ctp, family, ndoses = 4)
ctpm <- function(t, doses, interval, dose, weight) {
sum(sapply(0:(doses-1), function(n) ctp(t - n*interval, dose, weight)))
}
conc <- data.table(h = seq(0, 24, by = 0.1))
conc[, doses := pmin(h %/% 4, 3) + 1]
conc[, c1 := ctpm(h, doses, 4, 500, weight = 96), by = .(h, doses)]
conc[, c2 := ctpm(h, doses, 4, 500, weight = 64), by = .(h, doses)]
conc[, c3 := ctpm(h, doses, 4, 500, weight = 41), by = .(h, doses)]
conc[, c4 := ctpm(h, doses, 4, 250, weight = 23), by = .(h, doses)]
conc[, c5 := ctpm(h, doses, 4, 120, weight = 13), by = .(h, doses)]
ggplot(melt(conc[, -'doses'], id.vars = 'h'), aes(h, value, color = variable)) +
geom_line() +
scale_color_discrete(name = 'Weight', labels = c('DG', 'DH', 'DB', 'DB', 'DB')) +
theme(legend.position = 'top') +
geom_hline(yintercept = 10, color = 'black', linetype = 2, size = 1.25) +
geom_hline(yintercept = 20, color = 'black', linetype = 2, size = 1.25)> do.call(ctp, family, ndoses = 4)
> sd(do.call(ctp, rlnorm(2000)))

Source: Rawlins et al. (1977): Paracetamol (simplified)
> sd(do.call(ctp, rlnorm(2000)))
weight <- 70
meanlog <- log((weight * 0.6)^2 / sqrt(0.07^2 + (weight * 0.6)^2))
sdlog <- sqrt(log(1 + (0.07^2 / (weight * 0.6)^2)))
ggplot(data.frame(x = rlnorm(n = 2000L, meanlog, sdlog))) +
geom_histogram(aes(x)) +
ggtitle('Volume of distribution for 70 kg') + xlab('')
> sd(do.call(ctp, rlnorm(2000)))
for (i in 1:250) {
meanlog <- log((weight * 0.6)^2 / sqrt(0.07^2 + (weight * 0.6)^2))
sdlog <- sqrt(log(1 + (0.07^2 / (weight * 0.6)^2)))
conc <- copy(conc)[, c := ct(h, 1000, v = rlnorm(n = 1L, meanlog, sdlog),
k = 0.28, ka = 1.8, f = 0.89)]
(G <- G + geom_line(data = conc, color = 'gray', alpha = 0.1))
}
G + geom_line(color = 'black') + ggtitle('250 simulations')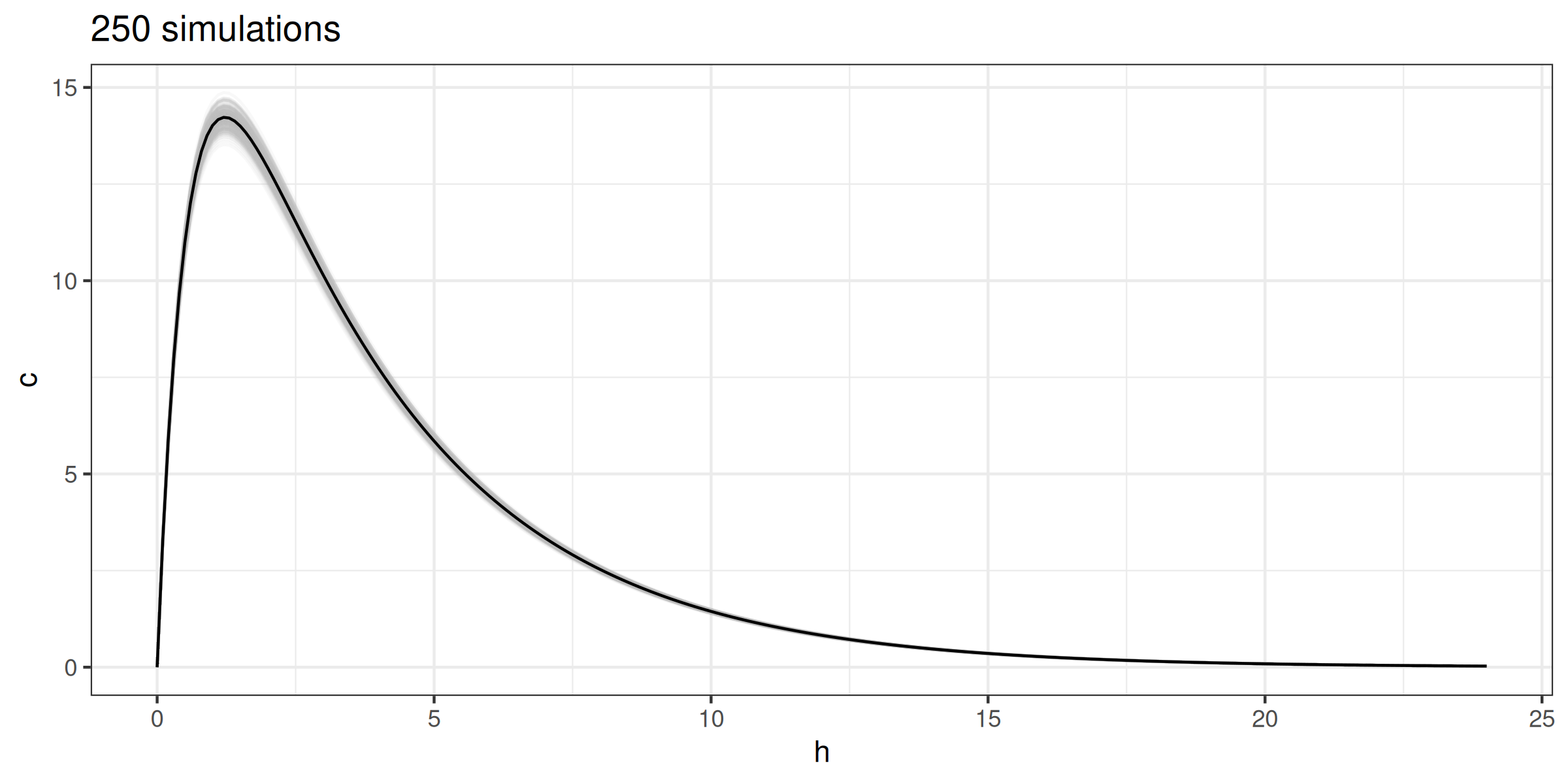
> sd(do.call(ctp, rlnorm(2000)))
simdata <- rbindlist(lapply(1:2000, function(i) {
meanlog <- log((weight * 0.6)^2 / sqrt(0.07^2 + (weight * 0.6)^2))
sdlog <- sqrt(log(1 + (0.07^2 / (weight * 0.6)^2))) * 5
as.data.frame(matrix(
ct(seq(0, 24, by = 0.1), 1000, v = rlnorm(n = 1L, meanlog, sdlog),
k = 0.28, ka = 1.8, f = 0.89),
nrow = 1))
}))
simagg <- data.frame(
h = seq(0, 24, by = 0.1),
min = apply(simdata, 2, FUN = min),
mean = apply(simdata, 2, FUN = mean),
max = apply(simdata, 2, FUN = max))
ggplot(simagg, aes(h)) +
geom_ribbon(aes(ymin=min, ymax=max), fill = 'gray') +
geom_line(aes(y = mean)) +
ylab('Blood concentration forecast') +
theme_bw() + theme(legend.position = 'top')> sd(do.call(ctp, rlnorm(2000)))

> fit(ctp, data.frame(conc = 5))
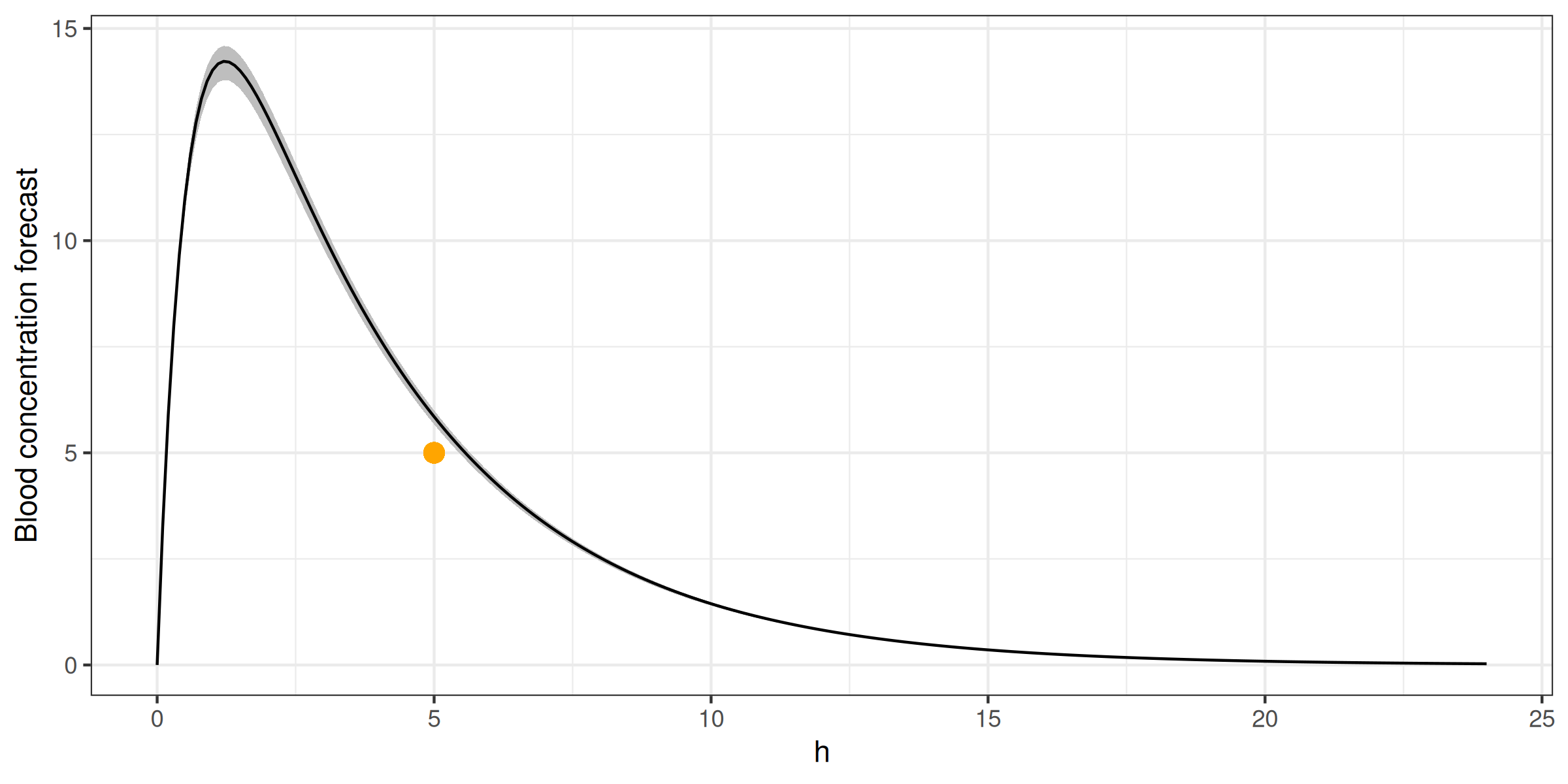
> fit(ctp, data.frame(conc = 5))
library(FME)
concentrations <- data.table(x = 5, y = 5)
model_function <- function(params, x) {
ct(x, dose = 1000, v = params['v'], k = 0.28, ka = 1.8, f = 0.89)
}
cost_function <- function(params) {
out <- model_function(params, concentrations$x)
concentrations$y - out
}
bay <- modFit(f = cost_function, p = c(v = weight * 0.6), method = 'Newton')
bayc <- copy(conc)[, c := ct(seq(0, 24, by = 0.1), 1000, v = bay$par[['v']],
k = 0.28, ka = 1.8, f = 0.89)]
ggplot(simagg, aes(h)) +
geom_ribbon(aes(ymin=min, ymax=max), fill = 'gray') +
geom_line(aes(y = mean)) +
geom_point(aes(x=5, y=5), color = 'orange', size = 3) +
geom_line(data = bayc, aes(y = c), color = 'orange') +
ylab('Blood concentration forecast') +
theme_bw() + theme(legend.position = 'top')> fit(ctp, data.frame(conc = 5))

> fit(ctp, data.frame(conc = 5))

> fit(ctp, data.frame(conc = 5))

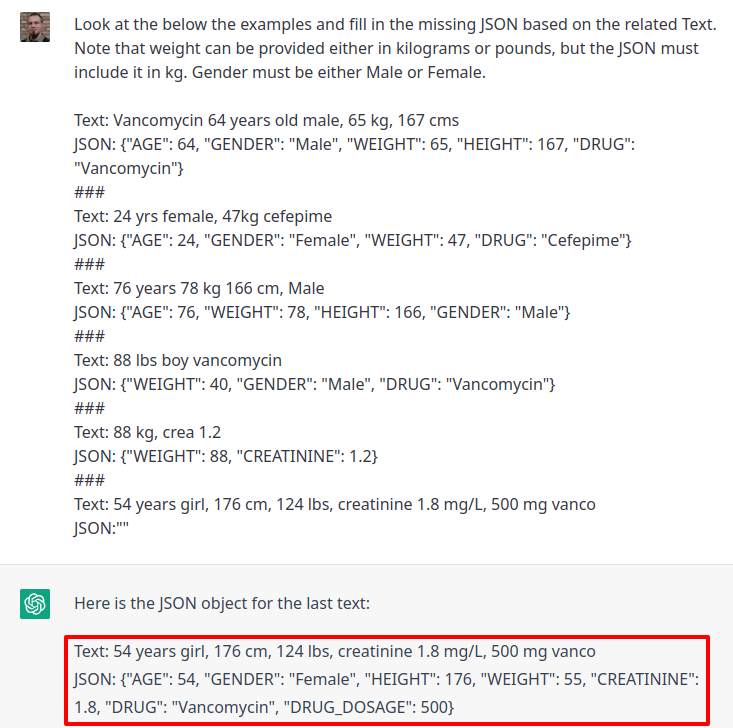
> library(chatgpt)
> library(chatgpt)
> library(chatgpt)

> library(chatgpt)

> library(chatgpt)

> library(chatgpt)

> library(chatgpt)
placeholder as cannot finish with an image